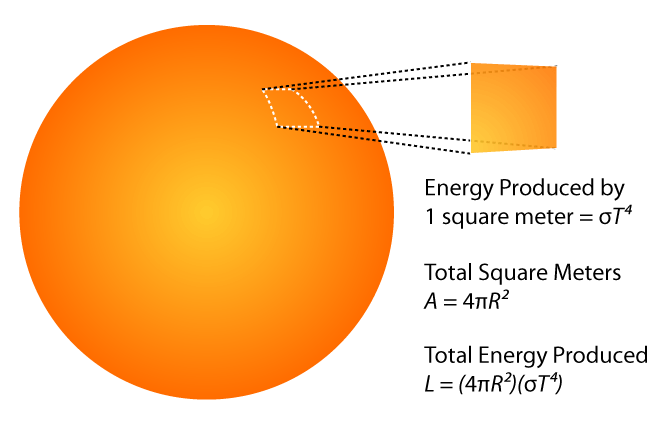L'andamento sperimentale dell'intensità della radiazione emessa in funzione della lunghezza d'onda era stato studiato alla fine dell'800 ma non c'era un modello teorico, basato sulla fisica classica, che lo potesse spiegare. Nel 1900 Planck elabora un modello basato sull'ipotesi non classica che il corpo nero emetta radiazione con un contenuto energetico discreto non continuo. L'ipotesi è davvero non classica. Infatti un regolatore di intensità luminosa di una lampadina può regolare l'intensità in modo continuo e non necessariamente a scatti. La radiazione emessa dal corpo nero invece ha energia E= nhν con n un numero intero. Quindi è possibile, per una certa frequenza ν, emettere radiazione di energia hν, 2hν, 3hν ecc. ma non 1.5hν.

$B_{\nu }\left(T\right)=\frac{2\mathrm{\pi h}{\nu }^3}{c^2}\frac{1}{e^{\raisebox{1ex}{$\mathrm{h\nu }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{kT}$}\right.}-1}$ (Wm^-2Hz^-1sterad^-1)

e l'intensità in relazione alla lunghezza d'onda, tenendo conto che $B_{\lambda }=\mid \frac{\mathrm{d\nu }}{\mathrm{d\lambda }}\mid B_{\nu }=\frac{c}{{\lambda }^2}{B}_{\nu }$ è:

$B_{\lambda }\left(T\right)=\frac{2\mathrm{\pi h}{c}^2}{{\lambda }^5}\frac{1}{e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\lambda kT}$}\right.}-1}$ (Wm^-3sterad^-1)

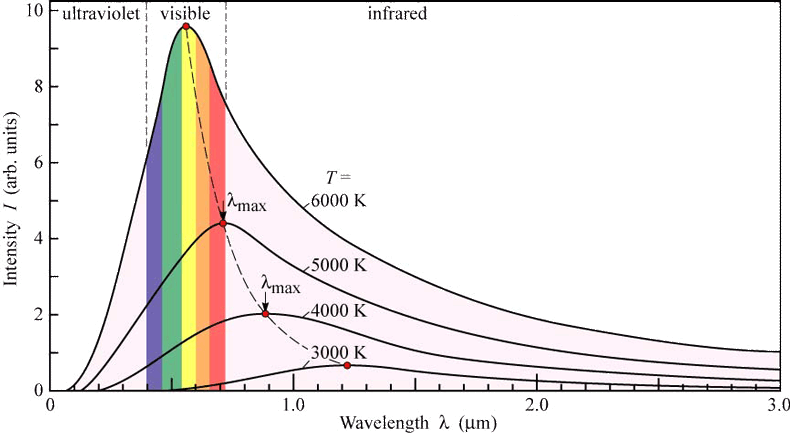
Una prima applicazione del modello di Planck è la spiegazione della legge di spostamento di Wien. Nel 1893 Wien aveva scoperto una relazione empirica tra la temperatura di un corpo radiante e la lunghezza d'onda alla quale si ha il massimo di intensità della radiazione emessa (legge di spostamento) :

${\lambda }_{max}=\frac{2.9·{10}^6}{T}$ nm

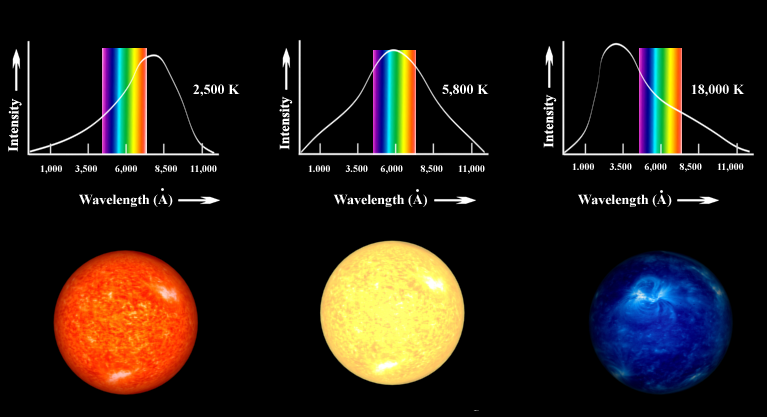
all'aumentare della temperatura del corpo radiante il massimo di emissione si sposta verso lunghezze d'onda più corte e frequenze più elevate (per questo motivo le stelle più calde sono blu e le stelle più fredde sono rosse).

Per ricavare la legge di Wien dalla formula di Planck occorre calcolare la derivata dell'intensità B_λ(T) rispetto λ e uguagliarla a zero. L'espressione che si ricava è:

$\frac{d{B}_{\lambda }\left(T\right)}{\mathrm{d\lambda }}=\frac{4{\pi }^2\hslash c^2\left[\left(2\pi \hslash c/\mathrm{kT\lambda }\right)e^{\raisebox{1ex}{$2\pi \hslash c$}\!\left/ \!\raisebox{-1ex}{$\mathrm{kT\lambda }$}\right.}-5(e^{\raisebox{1ex}{$2\pi \hslash c$}\!\left/ \!\raisebox{-1ex}{$\mathrm{kT\lambda }$}\right.}-1)\right]}{{\lambda }^6{(e^{\raisebox{1ex}{$2\pi \hslash c$}\!\left/ \!\raisebox{-1ex}{$\mathrm{kT\lambda }$}\right.}-1)}^2}=0$

I valori λ=0 e λ=∞ che soddisfano l'equazione corrispondono ai minimi della funzione B_λ(T). Per trovare il valore λ_max che corrispondente al massimo occorre risolvere l'equazione che deriva ponendo uguale a zero la parte di numeratore tra parentesi. Posto $x_0=\frac{2\pi \hslash c}{\mathrm{kT\lambda }}$ e sostituendo si trova l'equazione:

$x{e}^x-5(e^x-1)=0$

che deve essere risolta in modo numerico. La soluzione approssimata è x≃4.965, da cui sostituendo si trova la legge dello spostamento di Wien:

$T{\lambda }_{max}=\frac{2\pi \hslash c}{x_{0}k}\simeq 2.9·{10}^{-3}$ m°K

Un primo modello, sviluppato proprio da Wien, funzionava bene per piccole lunghezze d'onda (alte frequenze). Per ricavarlo Wien osservò che la curva di corpo nero assomigliava alla distribuzione delle velocità di Maxwell; suppose che le analogie fossero dovute al fatto che l’emissione di radiazione era in qualche modo legata proprio all’agitazione termica, e quindi alla velocità delle molecole del corpo nero e propose l'approssimazione, aggiustandone i parametri con l’aiuto dei dati sperimentali. La formula dell'intensità di radiazione ricavata da Wien può essere anche dedotta a partire dalla formula di Planck con l'opportuna approssimazione.

Quando la lunghezza d'onda della radiazione emessa è minore della lunghezza d'onda corrispondente alla massima intensità, λ_max si ha:

$\lambda <{\lambda }_{max}\to \lambda <\frac{\mathrm{hc}}{\mathrm{kT}}\to \frac{\mathrm{hc}}{\mathrm{kT\lambda }}>1\to e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\lambda kT}$}\right.}>1\to e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\lambda kT}$}\right.}-1\simeq e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\lambda kT}$}\right.}\to \frac{1}{e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{k\lambda T}$}\right.}-1}\simeq e^{-\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\lambda kT}$}\right.}$

Da cui l'approssimazione di Wien:

$B_{\lambda }\left(T\right)\simeq \frac{2h{c}^2}{{\lambda }^5}{e}^{\raisebox{1ex}{$-\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\lambda kT}$}\right.}$

dell'intensità della radiazione valida per lunghezze d'onda minori di λ_max. Per lunghezze d'onda maggiori l'approssimazione di Wien si allontana dalla curva sperimentale.

$\lambda \gg {\lambda }_{max}\to \lambda \gg \frac{\mathrm{hc}}{\mathrm{kT}}\to \frac{\mathrm{hc}}{\mathrm{\lambda kT}}\ll 1\to e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{\lambda kT}$}\right.}\simeq 1+\frac{\mathrm{hc}}{\mathrm{\lambda kT}}$

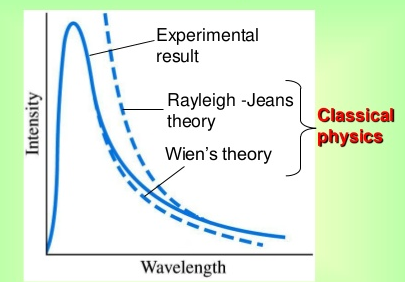
Sostituendo nella formula di Planck si ottiene l'approssimazione di Rayleigh-Jeans:

$B_{\lambda }\left(T\right)\simeq \frac{2h{c}^2}{{\lambda }^5}\frac{\mathrm{\lambda kT}}{\mathrm{hc}}=\frac{2\mathrm{ckT}}{{\lambda }^4}$

che approssima molto bene la curva sperimentale di Planck per lunghezze d'onda molto maggiori di λ_max.

L'approssimazione era stata precedentemente ricavata da Rayleigh che applicò il principio di equipartizione dell’energia al campo elettromagnetico che si instaura all' interno di una cavità risonante.

Una seconda applicazione è la legge di Stefan-Boltzmann (scoperta sperimentalmente da Stefan nel 1879 e spiegata teoricamente per la prima volta da Boltzmann nel 1884).

La legge di Stefan-Boltzmann stabilisce che la densità di flusso irradiata per tutte le frequenze è legata alla temperatura assoluta del corpo nero dalla relazione:

$F\left(T\right)=\sigma ·T^4$

dove σ è una costante universale detta costante di Stefan-Boltzmann.

Nella trattazione contemporanea la legge è ricondotta direttamente alla formula di Planck, di cui costituisce un integrale.

Consideriamo infatti l'intensità totale:

$B\left(T\right)={\int }_0^{\infty }{B}_{\nu }\left(T\right)\mathrm{d\nu }=\frac{2h}{c^2}{\int }_0^{\infty }\frac{{\nu }^3}{e^{\raisebox{1ex}{$\mathrm{h\nu }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{kT}$}\right.}-1}\mathrm{d\nu }$

Cambiando la variabile di integrazione a $x=\frac{\mathrm{h\nu }}{\mathrm{kT}}$ si ottiene $\mathrm{d\nu }=\frac{\mathrm{kT}}{h}\mathrm{dx}$ e , sostituendo, : $B\left(T\right)=\frac{2h}{c^2}\frac{k^4}{h^4}{T}^4{\int }_0^{\infty }\frac{x^3}{e^x-1}\mathrm{dx}$

La soluzione dell'integrale definito è : ${\int }_0^{\infty }\frac{x^3}{e^x-1}\mathrm{dx}=\frac{{\pi }^4}{15}$. Da cui $B\left(T\right)=\frac{2k^4}{c^2{h}^3}\frac{{\pi }^4}{15}·T^4=A·T^4$ con $A=\frac{2k^4}{c^2{h}^3}\frac{{\pi }^4}{15}$ .

La densità di flusso per una radiazione isotropica in un semispazio è (↑) : $F=\mathrm{\pi B}=\frac{2k^4}{c^2{h}^3}\frac{{\pi }^5}{15}{T}^4=\sigma T^4$ che è la legge di Stefan-Boltzmann.

Con la legge di Stefan-Boltzmann si può ricavare la relazione tra temperatura e flusso di radiazione (luminosità) di una stella. Se R è il raggio della stella l'area della superficie sarà 4πR². Da cui il flusso di radiazione L= 4πR²·F.

Supponendo la stella un radiatore perfetto come un corpo nero vale la legge di Stefan-Boltzmann F= σT⁴, da cui, sostituendo, il flusso di radiazione in funzione della temperatura è:

$L=4\mathrm{\pi \sigma }{R}^2{T}_e^4$

La temperatura T_e è la temperatura superficiale di una stella che irradia con la stessa densità di flusso totale di un corpo nero con la stessa temperatura. È detta temperatura effettiva della stella. Dalla legge di Stefan-Boltzmann si deduce anche che a parità di temperatura effettiva la stella con raggio maggiore ha maggiore luminosità e a parità di raggio la stella con la maggiore temperatura effettiva ha maggiore luminosità..

Si può porre la magnitudine bolometrica in funzione della temperatura effettiva.

Infatti ricordando (↑) la relazione di Pogson delle magnitudini bolometriche in funzione della luminosita:

$M_{\mathrm{bol}}-M_{\mathrm{bol},\odot }=-2.5\log \frac{L}{L_{\odot }}$

sostituendo la legge di Stefan-Boltzmann si trova la magnitdine bolometrica in funzione della raggio e della temperatura:

$M_{\mathrm{bol}}-M_{\mathrm{bol},\odot }=-2.5·\log \frac{R^2{T}^4}{R_{\odot }^2{T}_{\odot }^4}=-5·\log \frac{R}{R_{\odot }}-10·\log \frac{T}{T_{\odot }}$