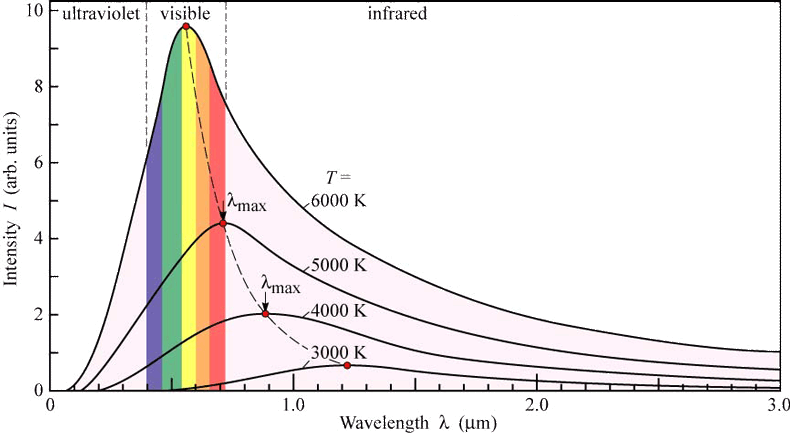
Le temperature delle stelle sono solitamente valutate confrontandole con un corpo nero. In realtà le stelle non irradiano proprio come un corpo nero ma il loro spettro è molto vicino a quello di un corpo nero. La più importante grandezza che descrive la temperatura superficiale di una stella è temperatura effettiva T_e che è la temperatura del corpo nero che irradia con lo stessa flusso luminoso totale della stella. Per calcolare la temperatura effettiva bisogna trovare il flusso luminoso totale integrato su tutte le frequenze e per questo motivo non è molto importante l'eventuale deviazione dallo spettro del corpo nero.

Con la legge di Stefan-Boltzmann si può ricavare la relazione tra temperatura e flusso di radiazione (luminosità) di una stella. Se R è il raggio della stella l'area della superficie sarà 4πR². Da cui il flusso di radiazione L= 4πR²·F.

Supponendo la stella un radiatore perfetto come un corpo nero vale la legge di Stefan-Boltzmann F= σT⁴ (↑), da cui, sostituendo, il flusso di radiazione in funzione della temperatura è:

$L=4\pi R^{2}F=4\mathrm{\pi \sigma }{R}^2{T}_e^4$

$F\text{'}=\frac{L}{4\pi r^2}=\frac{4\pi R^{2}F}{4\pi r^2}=\frac{R^2}{r^2}·F={\left(\frac{R}{r}\right)}^2·F={\left(\frac{\alpha }{2}\right)}^2·F$

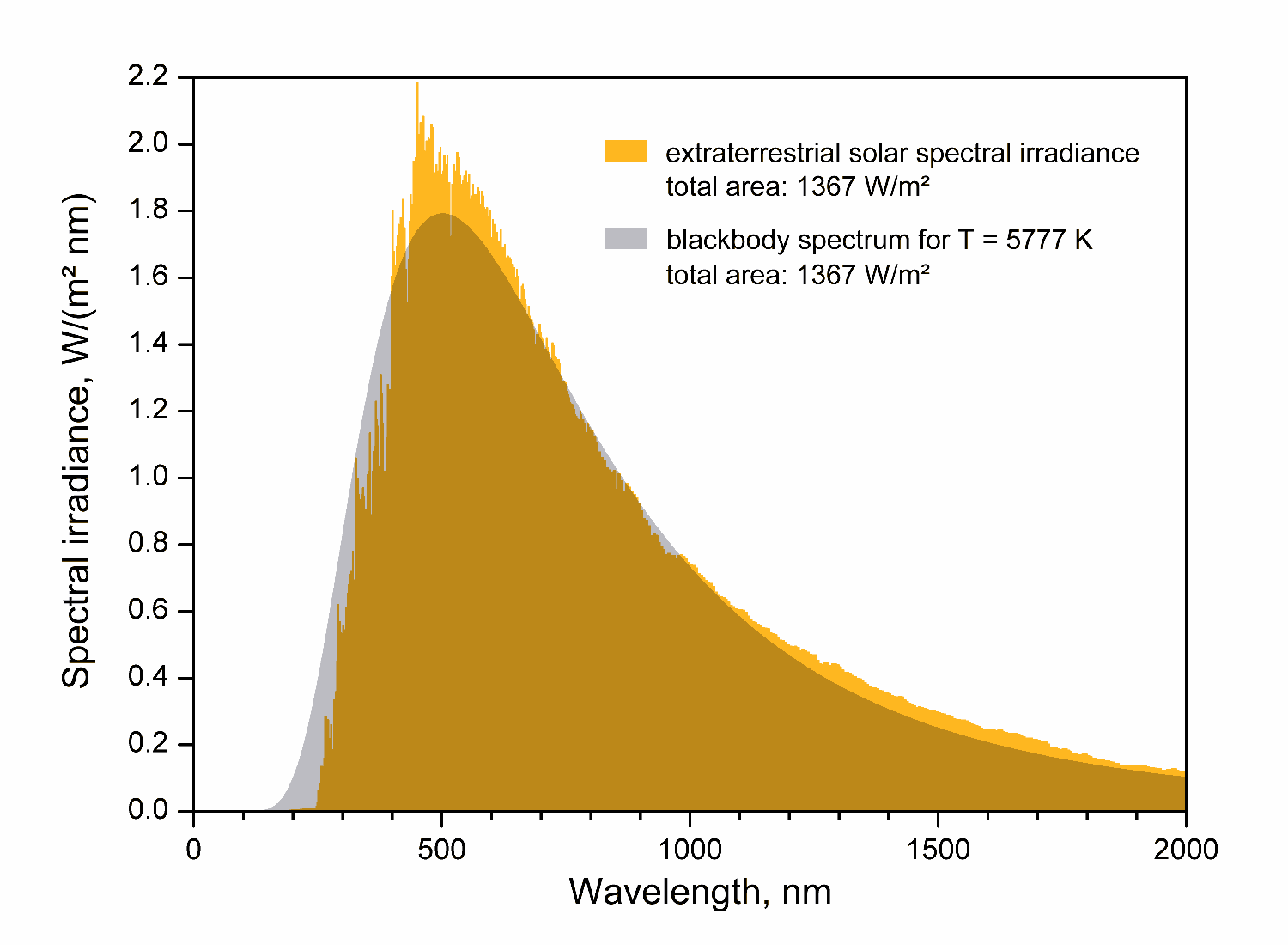
dove α=2R/r è il diametro angolare osservato. Quindi per conoscere la temperatura effettiva occorre misurare la densità di flusso totale e il diametro angolare della stella. Tuttavia è possibile conoscere questi dati solo in pochi casi e quando riesce a misurare il diametro angolare con misure di tipo interferometrico.

Se si assume che, per certe lunghezze d'onda, la densità di flusso F_λ corrispondente sulla superficie della stella può essere ricavata dalla legge di Planck la temperatura che si ricava è detta temperatura di brillanza T_b. Nel caso isotropico si ha F_λ= πB_λ(T_b) (↑) da cui la densità di flusso a distanza r:

$F_{\lambda }^{\text{'}}={\left(\frac{R}{r}\right)}^2{F}_{\lambda }={\left(\frac{\alpha }{2}\right)}^2\pi ·B_{\lambda }\left(T\right)$

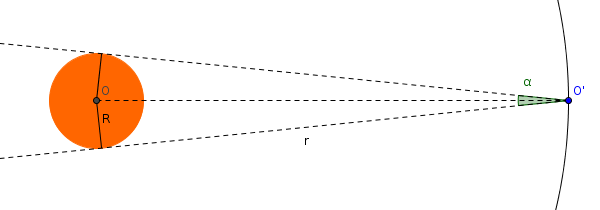
In radioastronomia le lunghezze d'onda sono molto grandi ed solitamente soddisfatta l'approssimazione di Rayleigh-Jeans ( eccetto che per le microonde) della formula di Planck (↑):

$B_{\nu }\left(T_b\right)=\frac{{\lambda }^2}{c}{B}_{\lambda }\left(T_b\right)=\frac{{\lambda }^2}{c}·\frac{2\mathrm{ck}{T}_b}{{\lambda }^4}=\frac{2k}{{\lambda }^2}{T}_b=\frac{2k{\nu }^2}{c^2}·T_b$

Nota l'intensità specifica monocromatica si può calcolare la temperatura di brillanza: $T_b=\frac{c^2}{2k{\nu }^2}{I}_{\nu }=\frac{{\lambda }^2}{2k}{I}_{\lambda }$

$T_A=\eta T_b$

η è l'efficienza del beam dell'antenna (in generale data un'antenna l'efficienza del beam è il rapporto tra la potenza ricevuta nel lobo principale e la potenza che sarebbe stata ricevuta se la potenza per unità di frequenza ricevuta fosse stata costante all'interno dell'angolo solido corrispondente al lobo principale. Tipicamente 0.4 ≤η≤0.8).

La temperatura di colore T_c è una temperatura che può essere calcolata senza la necessità di conoscere il diametro angolare.

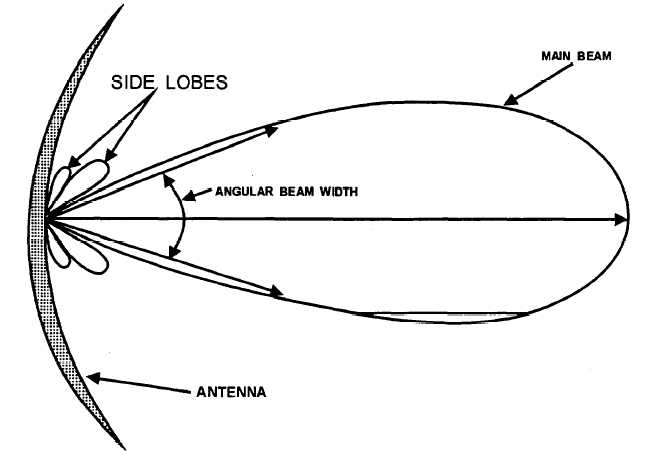
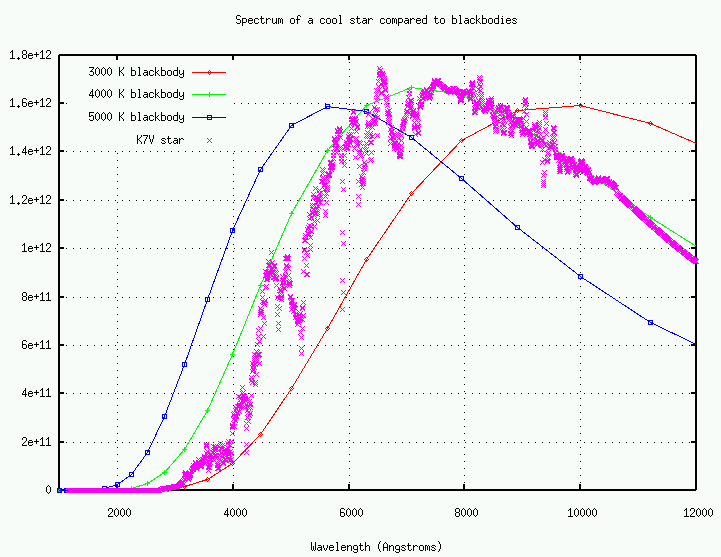
Bisogna confrontare la distribuzione spettrale della densità di flusso misurata con la corrispondente distribuzione spettrale del corpo nero calcolata a diverse temperature. La temperatura che corrisponde al miglior fit è la temperatura di colore nell'intervallo di lunghezze d'onda [λ₁,λ₂]. La temperatura di colore può essere diversa in diversi intervalli di lunghezza d'onda, dipende quale distribuzione spettrale di corpo nero si adatta alla distribuzione spettrale misurata in un particolare intervallo di lunghezze d'onda.

Un metodo semplice per calcolare la temperatura di colore è il seguente. Si misura la densità di flusso F'_λ a due lunghezze d'onda λ₁ e λ₂. Se si assume che la distribuzione dell'intensità segue la legge di Planck, il rapporto delle densità di flusso sperimentali deve essere lo stesso del rapporto delle densità di flusso teoriche:

$\frac{F_{\lambda 1}^{\text{'}}\left(T\right)}{F_{\lambda 2}^{\text{'}}\left(T\right)}=\frac{B_{\lambda 1}\left(T\right)}{B_{\lambda 2}\left(T\right)}=\frac{{\lambda }_2^5}{{\lambda }_1^5}\frac{e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{${\lambda }_2\mathrm{kT}$}\right.}-1}{e^{\raisebox{1ex}{$\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{${\lambda }_1\mathrm{kT}$}\right.}-1}$

La temperatura ricavata da questa equazione è la temperatura di colore T_c.

Le densità di flusso osservate corrispondono a certe magnitudini osservate m_λ1 e m_λ2 . Dalla definizione di magnitudini (↑):

$m_{\lambda 1}-m_{\lambda 0}=-2.5·\log \frac{F_{\lambda 1}^{\text{'}}}{F_{\lambda 10}^{\text{'}}}$ e $m_{\lambda 2}-m_{\lambda 0}=-2.5·\log \frac{F_{\lambda 2}^{\text{'}}}{F_{\lambda 20}^{\text{'}}}$

Da cui, sottraendo,: $m_{\lambda 1}-m_{\lambda 2}=-2.5·\log \frac{F_{\lambda 1}^{\text{'}}}{F_{\lambda 2}^{\text{'}}}+2.5·\log \frac{F_{\lambda 20}^{\text{'}}}{F_{\lambda 10}^{\text{'}}}=-2.5·\log \frac{F_{\lambda 1}^{\text{'}}}{F_{\lambda 2}^{\text{'}}}+\mathrm{const}$ . Il termine costante dipende dal diverso punto zero nelle diverse scale di magnitudini.

Se le temperature non sono molto alte (quindi λ_max non piccola) possiamo usare l'approssimazione di Wien (↑) per la regione visibile:

$m_{\lambda 1}-m_{\lambda 2}=-2.5·\log \frac{B_{\lambda 1}}{B_{\lambda 2}}+\mathrm{const}=-2.5·\log \left(\frac{e^{\raisebox{1ex}{$-\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{${\lambda }_1\mathrm{kT}$}\right.}}{e^{\raisebox{1ex}{$-\mathrm{hc}$}\!\left/ \!\raisebox{-1ex}{${\lambda }_2\mathrm{kT}$}\right.}}\frac{{\lambda }_2^5}{{\lambda }_1^5}\right)+\mathrm{const}=$

$=-2.5·\log {\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}^5+(\frac{\mathrm{hc}}{{\lambda }_1\mathrm{kT}}-\frac{\mathrm{hc}}{{\lambda }_2\mathrm{kT}})·2.5·\log e+\mathrm{const}=.$

$=-12.5·\log \frac{{\lambda }_2}{{\lambda }_1}+2.5\frac{\mathrm{hc}}{\mathrm{kT}}(\frac{1}{{\lambda }_1}-\frac{1}{{\lambda }_2})·\log e+\mathrm{const}.$

Il tutto può essere scritto nella forma: $m_{\lambda 1}-m_{\lambda 2}=a+\frac{b}{T_c}$

con $a=-12.5·\log \frac{{\lambda }_2}{{\lambda }_1}+\mathrm{const}.$ e $b=2.5·\log e\frac{\mathrm{hc}}{k}(\frac{1}{{\lambda }_1}-\frac{1}{{\lambda }_2})$. La formula mostra che vi è una relazione semplice tra la differenza delle magnitudini per due lunghezze d'onda e la temperatura di colore della porzione di distribuzione spettrale considerata.

La relazione che lega magnitudini mocromatiche e temperatura di colore è valida anche per gli indici di colore B-V (↑)