MISURA DELLE DISTANZE

METODI PER LA MISURA DELLE DISTANZE

( fonte principale: Karttunen et. al. Fundamental Astronomy - Springer)

LA PARALLASSE TRIGONOMETRICA. Il metodo della parallasse trigonometrica è basato sul moto annuale apparente delle stelle causato dal moto orbitale della Terra. Con questo metodo possiamo misurare dalla Terra distanze fino a circa 30 pc; è possibile andare oltre 30 pc e fino a circa 100 pc usando satelliti (Hipparcos e Gaia).

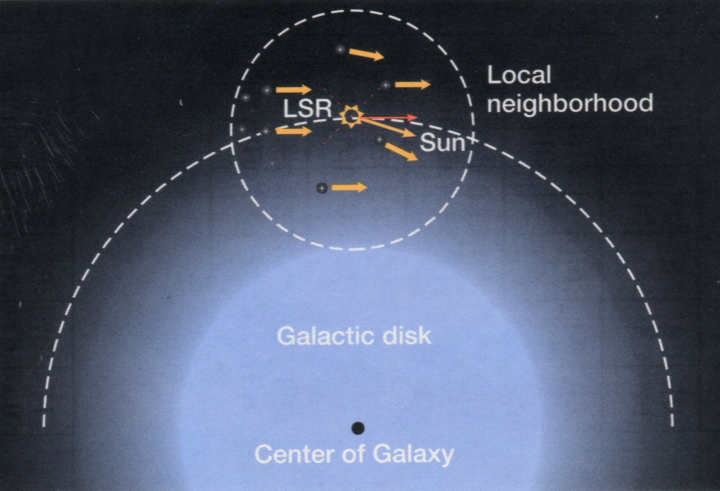
LA PARALLASSE STATISTICA. Il Sole si muove nello spazio e noi osserviamo le stelle da un sistema di riferimento in moto. Se le stelle si muovessero come il Sole, ovvero sia il Sole che le stelle ruotassero attorno il centro della Via Lattea con la stessa velocità angolare, allora non potremmo vedere muovere le stelle. Le stelle non avrebbero, rispetto a noi, un moto proprio. Ma in realtà le stelle hanno un moto proprio perchè tutte le stelle nella Galassia (e con esse il Sole) anche se ruotano intorno al centro galattico, a causa della mutua attrazione gravitazionale esercitata dalle stelle vicine, posseggono un ulteriore moto casuale. La velocità delle stelle ripetto al centro galattico è detta "velocità peculiare rispetto al centro galattico".
Per effetto di questo moto proprio vediamo alcune stelle avvicinarsi, altre allontanarsi da noi. La velocità di avvicinamento o allontanamento è la velocità radiale ovvero la velocità lungo direzione di osservazione. Poi c'è una velocità tangenziale: la velocità angolare che è uguale a quella tangenziale diviso la distanza, è detta velocità del moto proprio.

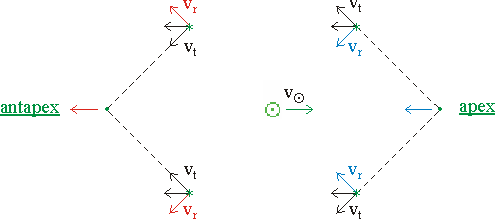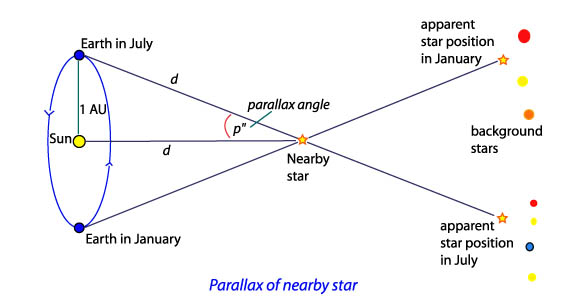
Possiamo decidere che la velocità di avvicinamento è negativa e quella di allontanamento positiva. Consideriamo ora la stella che ha la più piccola velocità radiale ovvero la più grande velocità di avvicinamento. È come se noi ci stiamo dirigendo proprio su quella stella. Quella stella individua l'apice, nel verso opposto abbiamo l'antiapice. Poichè le stelle sono distribuite casualmente ci aspettiamo che quelle vicino all'apice hanno una velocità media di avvicinamento elevata, quelle vicino all'antiapice una velocità media di allontanamento elevata e quelle che sono su una circonferenza centrata sul Sole e perpendicolare alla direzione apice-antiapice, in media, non si avvicinano nè si allontanano, e quindi hanno una velocità radiale media nulla. Però le stelle che sono su questa circonferenza hanno, in media, un moto proprio ovvero una velocità tangenziale diversa da zero. Anzi, in media, il moto proprio è l'unica velocità e quindi il moto proprio delle stelle in questa circonferenza è grande (mentre quello delle stelle vicino apice e antiapice è piccolo).

Ora definiamo un nuovo sistema di riferimento, il Sistema Locale a Riposo. Per definirlo consideriamo un punto per cui la velocità media di tutte le stelle vicino al Sole (compreso il Sole) rispetto questo punto è nulla. La velocità media delle stelle vicino al Sole rispetto al Sole non è nulla. E anche il Sole rispetto al SLR ha una sua "peculiare" velocità. Quindi, istantaneamente rispetto al SLR la velocità media delle stelle vicino al Sole è uguale ed opposta a quella del Sole. La velocità delle stelle rispetto al SLR è detta "velocità peculiare rispetto al SLR". Il SLR è "a riposo" solo rispetto alle stelle vicino al Sole con le quali è calcolato. Ma il SLR si muove attorno al centro della Via Lattea. La velocità del Sole rispetto le stelle vicine è di 20 km/s.

Che utilità ha il SLR per poter calcolare la distanza di stelle lontane ? In effetti il moto proprio del Sole può essere usato per ricavare la distanza delle stelle perchè il raggio dell'orbita terrestre è troppo piccolo come linea di base per misurare la parallasse trigonometrica (in un anno il Sole percorre nel suo moto intorno al centro della Galassia una distanza pari a quattro volte il raggio dell'orbita terrestre).

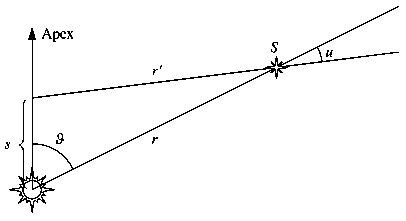Consideriamo infatti una stella con una distanza angolare θ rispetto all'apice e che è a distanza r dal Sole . Applicando il teorema dei seni al triangolo di figura si trova:

$\frac{r^{'}}{\sin θ} = \frac{s}{\sin u}$

con s lo spostamento del Sole nell'intervallo di tempo t e u lo spostamento angolare della stella rispetto al Sole. Poichè u è molto piccolo si può ricavare che :

$r = \frac{s \cdot \sin θ}{u} = \frac{\frac{s}{t} \cdot \sin θ}{\frac{u}{t}} = \frac{V_{s}}{μ_{A}} \cdot \sin θ$

V_s è la velocità del Sole rispetto al centro galattico e μ_A è la velocità angolare della stella osservata rispetto al Sole misurate in un tempo t.

In questo schema è stata considerata solo la velocità angolare della stella come se fosse ferma. Ma la stella ha una velocità peculiare rispetto al centro della Via Lattea e quindi il suo moto proprio non è solo la componente μ_A ma è presente anche la velocità peculiare. La formula precedente non fornisce una distanza corretta. Se però si considera il moto del SLR al posto di quello del Sole e se si considera un campione di stelle tutte quasi alla stessa distanza dal Sole (e quindi anche dal SLR), la media dei diversi r trovati ci fornisce la distanza corretta perchè l'effetto medio delle velocità peculiari rispetto al SLR è nullo.

Ma come si fa a sapere che un gruppo di stelle sono alla stessa distanza dal Sole ? Se sappiamo a priori che un gruppo di stelle ha la stessa magnitudine assoluta M dalla relazione tra le magnitudini:

m - M = 5 \cdot \log (\frac{r}{10 pc}) + A (r)

le stelle che hanno la stessa magnitudine apparente m sono alla stessa distanza. E quali stelle soddisfano la condizione di avere la stessa magnitudine assoluta ? Le stelle della sequenza principale del tipo A4, le variabili RR lyrae, le cefeidi con un particolare periodo, le stelle negli ammassi. Per esempio questo metodo è stato usato per determinare la distanza delle Iadi.

IL FITTING NELLA SEQUENZA PRINCIPALE. Confrontando la sequenza principale di un ammasso aperto a distanza nota (ad esempio le Iadi) nel diagramma "magnitudine assoluta - colore", con la sequenza principale nel diagramma "magnitudine apparente - colore" di un ammasso di cui non si conosce la distanza, si può risalire alla distanza di quest'ultimo. Di quanto dobbiamo spostare nella direzione verticale il secondo diagramma per portare a coincidere esattamente le due sequenze principali è la quantità M-m, ovvero il modulo di distanza dell'ammasso aperto a distanza incognita.
Di nuovo, usando la formula:

$m - M = 5 \cdot \log (\frac{r}{10 pc}) + A (r)$

è possibile ricavare la distanza r. Chiaramente questo metodo funziona se le stelle negli ammassi hanno quasi la stessa distanza.

LE PARALLASSI FOTOMETRICHE. Nel metodo delle parallassi fotometriche le distanze sono determinate usando direttamente la formula $m - M = 5 \cdot \log (\frac{r}{10 pc}) + A (r)$ . Il metodo è condizionato da dover conoscere la magnitudine assoluta M e, allo scopo, ci sono diversi metodi per misurarla. Per esempio le magnitudini assolute delle cefeidi si possono ottenere dal loro periodo. Le magnitudini assolute delgi ammassi possono essere ricavate con il metodo del fitting nelle sequenza principale.

Le parallassi trigonometriche non vanno molto lontano. Anche con l'uso del satellite Hipparcos sono state determinate le distanze di poche cefeidi. Il metodo della parallasse statistica è indispensabile per misurare la magnitudine assoluta di oggetti brillanti più lontani. Quando si riesce a farlo si uò usare il metodo fotometrico per misurare le distanze di oggetti ancora più lontani.